현재 난류의 미스터리에 대한 연구결과
댓글
0
조회
4
10시간전
작성자 :
 갓파
갓파
 갓파
갓파
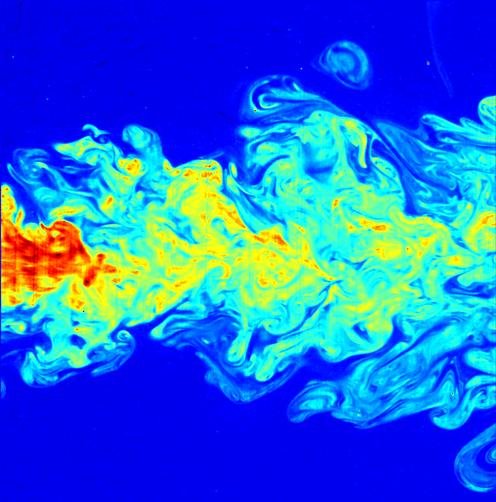
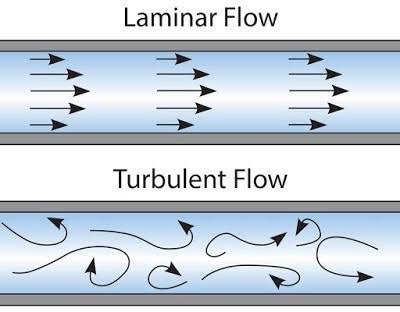
난류라는게 있음
얘는 똑바로 가지못하고
뭔가 ㅈㄴ 난리치면서 가는 애임
똑바로 가는애랑 비교하면
난리가 나버린게 그냥 눈에 보임
근데 이거 자연현상이라
물체가 움직이기만해도 크고작은 난류가 자꾸 생김
맨날 난리났다고 무시하기엔
너무 흔하게 발생함
그래서 사람들이 얘는 뭘까? 싶어
F=ma부터 시작해서 유체를 계속 분석하며
이론적인 공식을 만들었고 수정의 수정을 거쳐
최종적인 근본식을 만듦
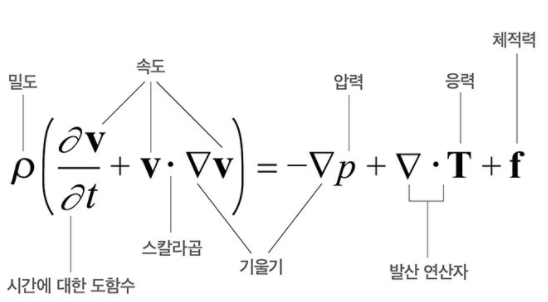
그게 공대생들의 개꿀잼 파트인
나비에-스토크스 방정식임
이건 대부분 유체의 움직임을 설명해주는
가장 근본적인 공식임
문제는
수학적이고 과학적이고 이론적으로 열심히
만들긴 만들었는데
좀 말도안되게
현실에서 발생하는 거의 모든 거시적인 유체현상을
ㅈㄴ 소름돋을 정도로 완벽에 가깝게 설명해줌
잘 맞아떨어져서 잘 사용하고 있는데
그거와 반대로 몇몇 사람들은
이 식 정말 완벽한거 맞는가? 에 대해 의문을 품었고
식의 오류를 발견하거나 완벽한걸 증명하면
14.60억원을 주는 7대 난제로도 등록됨
이걸 증명하는게 어려운 이유는
단순하게 공식을 푸는게 너무 너무 어려움
풀면 풀수록 계산량이 폭발해버려서
현시대의 슈퍼컴퓨터 + Ai 로도 아직 완벽하게 못다룸
그러니 너무 정직하게 푸는건 어려우니
차라리 계산방식을 우회 하자면서
여러 창의적인 방식이 나오고 있고
최근 유망한 단서를 찾음
구글 딥마인드에서 Ai모델을 학습시켜
간접적으로 탐색하는 방식으로 연구했고
불안정한 특이점이 있는거 같다고 분석했지만
말그대로 있는거 같다 이지 정밀한 증명이 아니라
완전히 증명됐다고는 못하는 중임
그래서 나비에-스토크스 식을 우회하던지 변형하여
풀기 쉽게 만드는 방식이 많은데
그 중 하나가 콜모고로프가 생각한 방식임
방정식을 직접 푸는건 어려우니
난류라는 존재의 패턴을 찾아보자 하면서
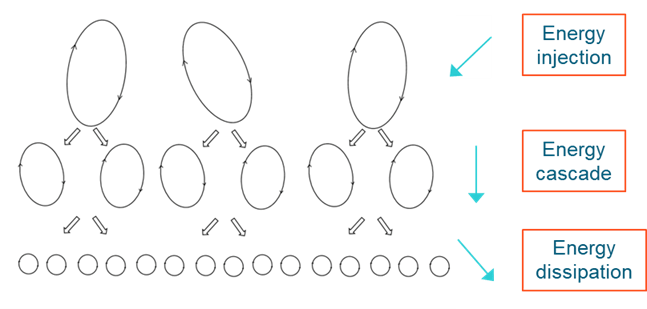
난류 속에서 큰 소용돌이가 깨져 작은 소용돌이가 되고
걔네가 또 깨져 더 작은 소용돌이가 되는데
이런 과정을 설명할 수 있는
보편적인 법칙이 없나 싶어서 찾은게
다들 알고있는 -5/3 법칙임
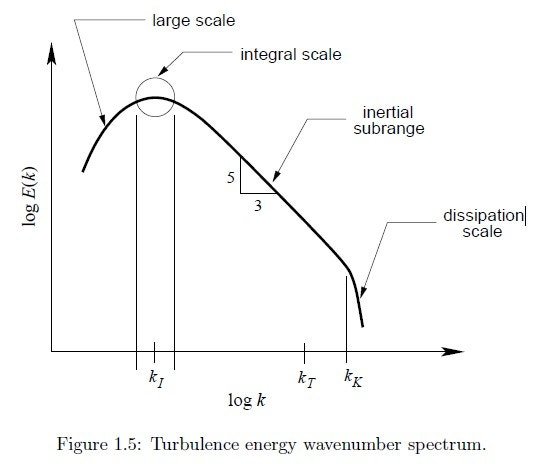
이는 완벽한건 아니지만 대부분의 소용돌이는 소산될수록 관성영역에서
에너지 밀도가 -5/3승 비율로 줄어든다는 법칙이고
그래도 보편적인 규칙이라 웬만한건 다 들어 맞았는데
아무리 끼워맞춰도 뭔가 다른 패턴을 가진 놈이 있었음
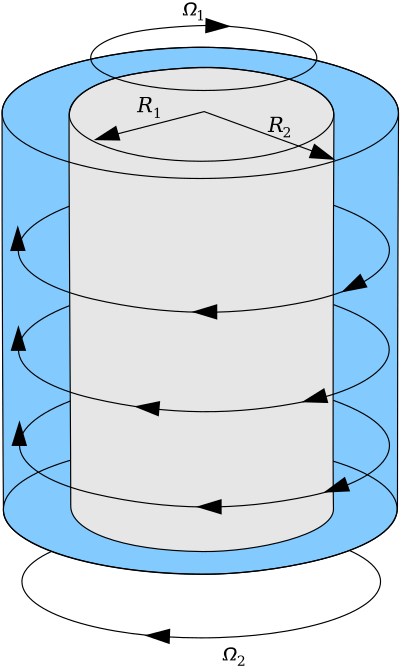
테일러-쿠에트라는 놈임
얘는 원통을 기준으로 빙글빙글 도는 단순해보이는 앤데
여러 분석을 해봐도 -5/3 법칙을 따르지 않는걸로 나옴
그래서 이건 아예 다른 영역이구나 로 결론 내리고
크게 신경안쓰고 있었는데
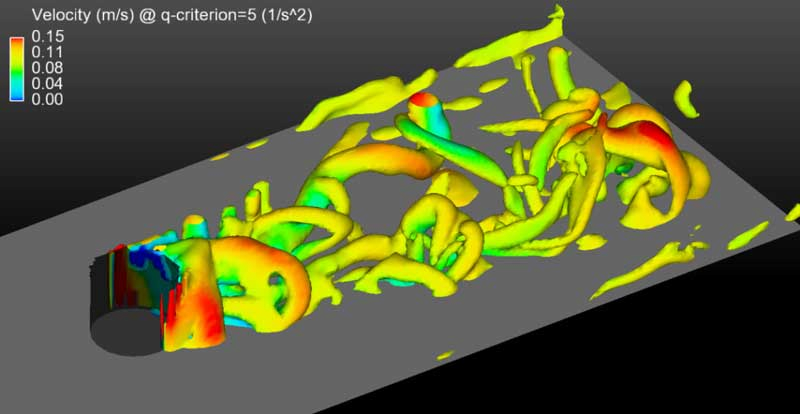
누가 최첨단 분석기기를 사용하여
플라잉-와이어 방식으로 분석해봄
기존방식은 벽에 센서를 달고
소용돌이가 발생하면 분석하는거 였는데
플라잉-와이어 방식은 센서를 벽에 안달고
소용돌이랑 같이 돌아다니는 방식을 사용하여 데이터를 수집함
이러한 장비교체를 통해
여러 잡음의 존재를 효과적으로 제거했고
난류 속 아주 작은 소용돌이의 미세한 속도변화를 깔끔하고 정밀하게 측정하며
고해상도 데이터를 수집할 수 있게 됨
새로운 관점에서 데이터를 해석할 수 있게 바꾼거임
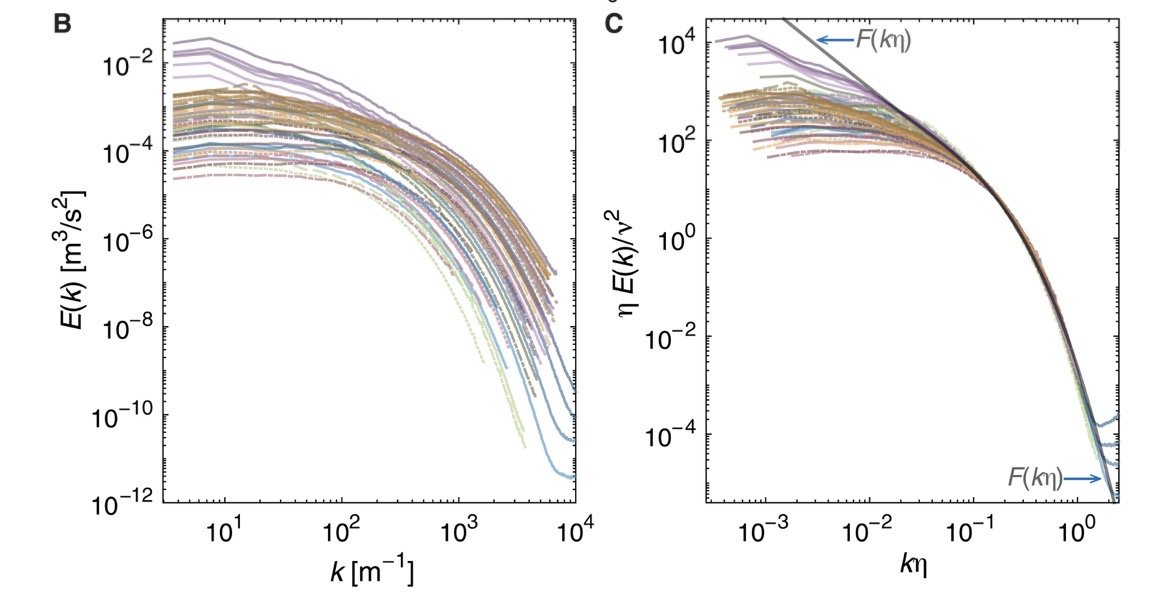
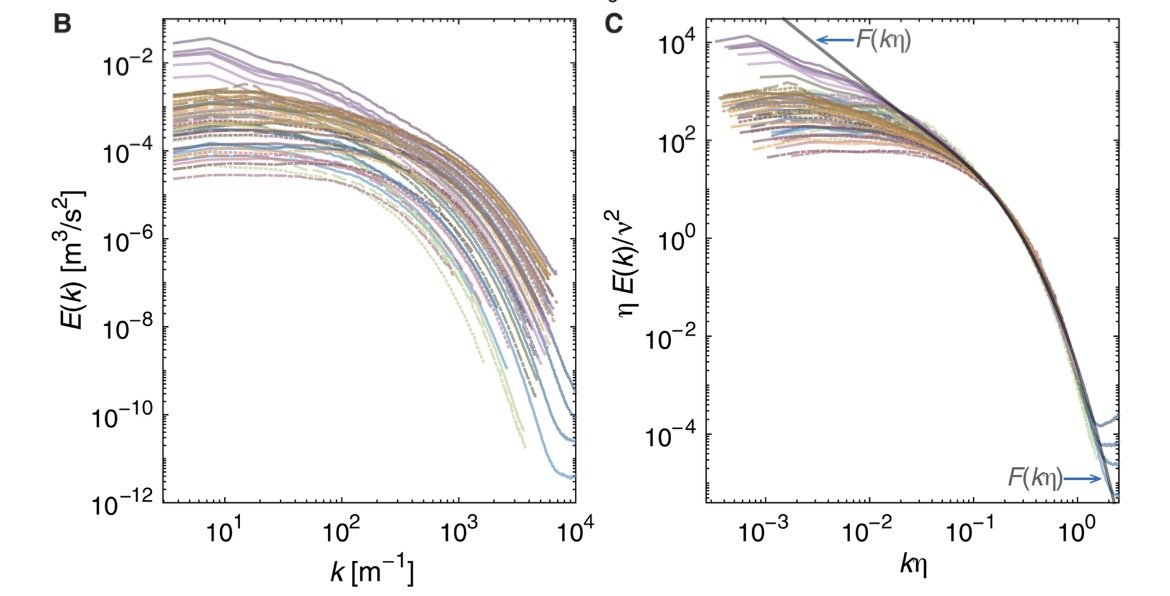
일단 기존 과학자들이 기준으로 삼던 부분을 보면
가로축 소용돌이 크기
세로축 에너지
로 정의내린 후 -5/3 이 적용되는 중간지대인
관성영역에만 집중했음
그런식의 데이터 기준을 잡아버리니
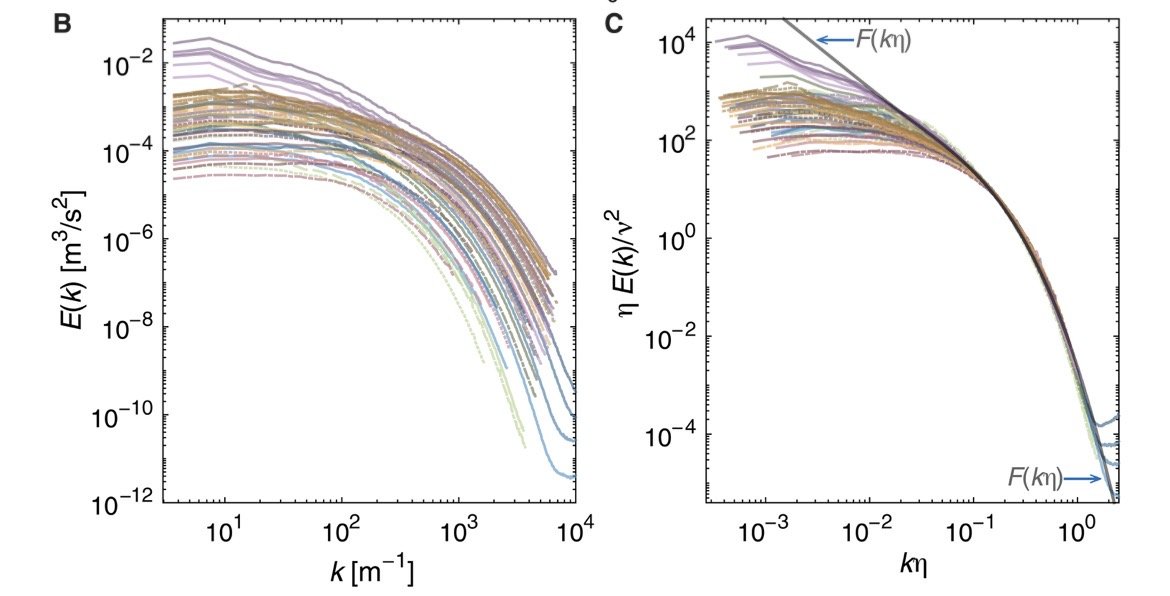
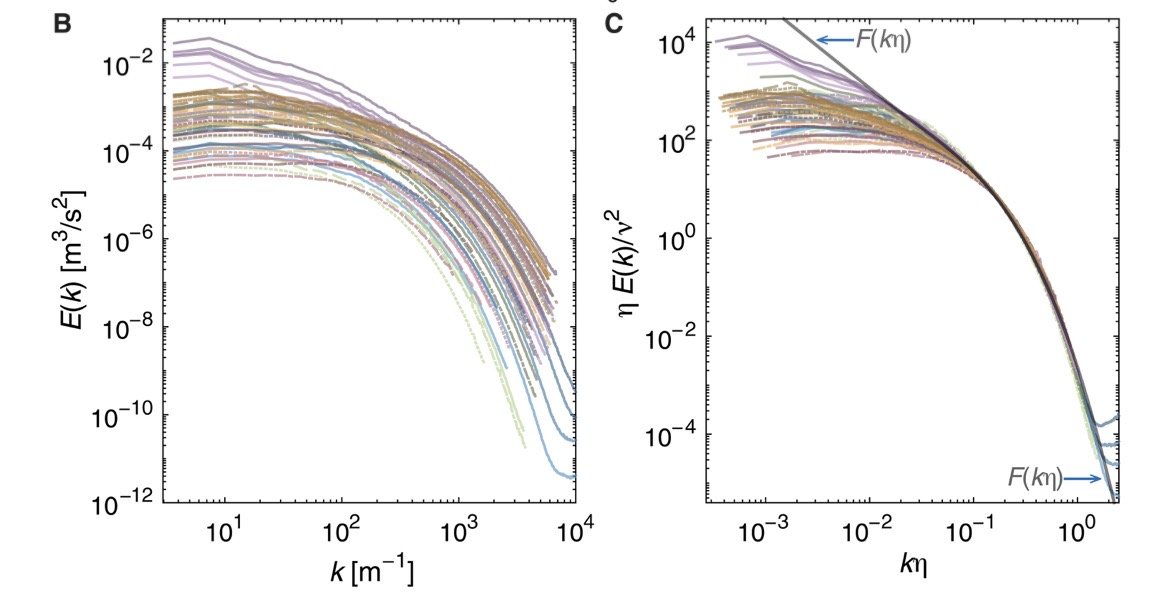
위의 왼쪽 그래프를 보면 소용돌이마다
곡선형태가 다르고 규칙성이 크게 나타나지 않았음
왼쪽처럼 뭔가 난잡하고 이상하니
테일러-쿠에트 난류는 규칙성이 크게 없다로 생각했었는데
생각해보면 난류라는건 체급이란게 존재해서
스케일에 따라 난류의 특성과 성격이 많이 달라짐
이런 스케일을 하나하나 고려하지 않고
그래프에 박아 넣으니
전부 제각각으로 나타날 수 밖에 없었는데
각자의 난류는 고유의 최소 에너지 소모 단위인
고유의 콜모고로프 길이 η 를 가지고 있다는 점을 고려하여
여러 조건에서 측정한 실험데이터들을
동일한 기준으로 쳐다보게 재조정하는 정규화 과정인 데이터 붕괴를 도입함
오른쪽 그림을 보면 가로축에 η 가 곱해진게 보이는데
이렇게되면 가로축은 무차원수가 되기 때문에
상대적인 값으로 표현할 수 있음
세로축도 마찬가지
이런식의 정규화를 했더니 완전히 달라보였던 값들이
하나의 선처럼 모여들었고
보편적인 곡선과 일치하는 것을 보여줌
즉, 테일러-쿠에트 흐름은 -5/3 법칙을 따르지 않고 제각각이여서
규칙성이란게 없는 아예 별종으로 취급했지만
보편적인 기준축으로 다시 분석해보니
그보다 더 근본적인 콜모고로프의 보편성을 따르며
규칙성을 지니고 있다는 증거를 제시한 셈임
혼자만 따로 노는 외톨이 현상이 아니라
모든 난류와 똑같은 난류의 근본 물리법칙을 따르는 애 였다는 거임